Because no light passes through the two polarizers initially, their axes must be perpendicular to one another. Let
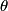 denote the angle between the middle polarizer and the first one. Then, the middle polarizer reduces the intensity the light that passes through it by a factor of denote the angle between the middle polarizer and the first one. Then, the middle polarizer reduces the intensity the light that passes through it by a factor of 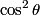 . And the last polarizer reduces the intensity of light that passes through it by a factor of . And the last polarizer reduces the intensity of light that passes through it by a factor of 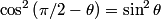 . So, the intensity of light that passes through all three is . So, the intensity of light that passes through all three is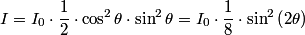 The factor of 1/2 comes from the fact that any polarizer reduces the intensity of unpolarized light by a factor of 1/2. 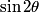 is maximized when is maximized when 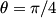 , and it has a maximum value of 1. So, the maximum fraction of incident power transmitted is 1/8. Hence answer (B) is correct. , and it has a maximum value of 1. So, the maximum fraction of incident power transmitted is 1/8. Hence answer (B) is correct. |